Baby-Ligero: Three Tiny Tests for a Tiny Circuit

TL;DR — I took Muthu Venkitasubramaniam's Ligero whiteboard session (ZK Hack S3M5) and distilled the core idea into a tiny Rust lab:

Encode a toy circuit z = x * y + x over a small field.

Arrange its wires into rows of a matrix U, each row a tiny Reed-Solomon (RS) codeword.

Implement the three Ligero-style tests on the rows:

a proximity test that only checks “are you in the code?”,

a multiplication test that checks t = x*y,

a linear test that checks z = t + x.

Craft a cheating strategy that passes proximity + linear, and see empirically that:

one round of tests catches it with probability ≈ 1/p,

repeating with fresh randomness drives cheating probability down like ≈ (1/p)^k.

All the code built for this study session can be found on github: ligero-mini-lab.

1. Motivation

In week 5 of my ZK learning plan (following the ZK Hack Whiteboard Sessions), I watched Muthu Venkitasubramaniam explain Ligero. The part that really grabbed me:

Ligero is not "just another polynomial-commitment SNARK".
It comes from the MPC-in-the-head paradigm, but what you actually see in the protocol are:
- a big matrix U of codewords (rows),
- three simple tests defined as random linear combinations of those rows:
  - proximity (are you close to a code?),
  - multiplication (are the products consistent?),
  - linear (do linear constraints hold?).

He claims that if you understand this U + tests picture, you're basically one step away from a full zero-knowledge SNARK with succinct verification.

So my goal for this week was:

Build a baby Ligero in Rust that actually runs those three tests on a tiny circuit, and see soundness amplification in numbers.

No MPC, no full pre-processing SNARK — just enough structure to internalize what those three tests are really doing.

2. From Ligero to a Baby Model

In the talk, Muthu considers a vector witness

$w = (x, y, z)$ with $x, y, z ∈ F^m$ ,
and constraints of the form $x ⊙ y = z$ (coordinate-wise multiplication).

He then packs everything into a matrix U with 3m rows, each row a vector u_i ∈ F^n that lives in a linear code (think Reed-Solomon).

On this U, he defines three tests with a random challenge r:

Proximity test:
$V_p = \sum r^i u_i$ where the weight vector is $(1, r, r², …, r^{3m})$ .

The verifier checks that $V_p$ “reconstructs correctly” as a codeword (low-degree polynomial) → proximity to RS code.
Multiplication test:
$V_m = \sum_{i=1}^{m} r^i (u_{3i-2} ⊙ u_{3i-1} - u_{3i})$ .

Each triple $(u_{3i-2},u_{3i-1},u_{3i})$ encodes $(x_i, y_i, z_i)$ ; the test checks all $x_i*y_i=z_i$ at once.
Linear test:
$V_\ell = \sum_{i=1}^{3m} r^i \hat{r}[i]\,u_i$ where $\hat{r} = (1,r,r^2,\dots)A$ .

This enforces the linear constraints $A w = b$ on the encoded rows.

My "baby Ligero" does a tiny version of this:

I pick a small prime field $F_p$ with p = 97.
I pick very small parameters:
- m = number of “gates” / coordinates (e.g. 4),
- n = codeword length (e.g. 7).
I build a matrix U whose rows are RS codewords (evaluations of low-degree polynomials).
I implement:
- a proximity test with V_p,
- a multiplication test with V_m,
- a linear test for a specific constraint.

Then I simulate an honest prover and a clever cheating prover and watch the tests behave.

3. Tiny Field and Reed-Solomon Machinery

3.1 Field $F_p$ with a Small Prime

For this lab I use a small prime modulus p = 97, mainly so I can debug by eye:

/// Small prime field F_p used throughout the Ligero mini lab.
#[derive(Copy, Clone, Debug, PartialEq, Eq, Hash)]
pub struct F {
    /// Always kept reduced modulo P.
    pub const P: u32 = 97;
    value: u32,
}
 
impl F {
    pub fn from(x: u32) -> Self {
        Self { value: x % Self::P }
    }
 
    pub fn as_u32(self) -> u32 {
        self.value
    }
 
    pub fn pow(self, mut exp: u64) -> F {
        let mut base = self;
        let mut acc = F::from(1);
        while exp > 0 {
            if exp & 1 == 1 {
                acc = acc * base;
            }
            base = base * base;
            exp >>= 1;
        }
        acc
    }
 
    pub fn inv(self) -> F {
        assert!(self.value != 0, "no inverse for 0");
        // Extended Euclidean algorithm returns s such that s * self ≡ 1 (mod P).
        eea_inv(self)
    }
}

The inverse uses the Extended Euclidean Algorithm (EEA):

Standard Euclidean algorithm computes gcd(a, p) via repeated remainders.
EEA also tracks coefficients s, t with: $s \cdot a + t \cdot p = \gcd(a, p)$
Over a prime field, gcd(a,p)=1 for any non-zero a, so: $s \cdot a + t \cdot p = 1 \quad \Rightarrow \quad s \cdot a \equiv 1 \mod p$ and s is the modular inverse of a.

So F::inv is literally "EEA on a and p, return the s".

3.2 Reed–Solomon: Evaluate / Interpolate / Low-degree Check

I fix a tiny RS domain:

pub struct Domain {
    pub points: Vec<F>,
}
 
impl Domain {
    pub fn new_n(n: usize) -> Self {
        // α_j = j for j=0..n-1 in F_p
        let points = (0..n).map(|j| F::from(j as u32)).collect();
        Self { points }
    }
 
    pub fn len(&self) -> usize {
        self.points.len()
    }
}

Then three basic operations:

Evaluate a polynomial on the domain:

pub fn eval_poly(coeffs: &[F], domain: &Domain) -> Vec<F> {
    domain.points.iter().map(|&x| {
        let mut acc = F::from(0);
        let mut power = F::from(1);
        for &c in coeffs {
            acc = acc + c * power;
            power = power * x;
        }
        acc
    }).collect()
}

Interpolate a polynomial of degree < deg_bound from evaluations (or return None if inconsistent):

pub fn interpolate_poly(values: &[F], domain: &Domain, deg_bound: usize) -> Option<Vec<F>> {
    let n = domain.len();
    if deg_bound >= n {
        return None; // cannot uniquely interpolate
    }
 
    // Solve Vandermonde system for coefficients c_0..c_deg_bound
    // If there's a unique solution, return it; otherwise None.
    // (I use a simple Gaussian elimination in the lab.)
    // ...
}

Low-degree test: "Is this vector a codeword of degree < deg_bound?":

pub fn is_low_degree(codeword: &[F], domain: &Domain, deg_bound: usize) -> bool {
    if let Some(coeffs) = interpolate_poly(codeword, domain, deg_bound) {
        // Re-evaluate and check it matches exactly
        let roundtrip = eval_poly(&coeffs, domain);
        roundtrip == codeword
    } else {
        false
    }
}

Intuition:

An RS codeword is just "evaluation of a low-degree polynomial on a fixed domain".
If a vector passes is_low_degree, it lies on the code (not necessarily close — my lab is stricter than the real thing, which allows small errors).
Ligero uses this to express “U is close to a code” via random linear combinations.

In my baby setting, proximity = "exact RS codeword", because I want to see the tests clearly, not deal with noise.

4. Building the Tableau for a Single Gate

Start with a tiny circuit:

z = x \cdot y + x \quad \text{over } F_{97}

I introduce an intermediate wire $t=x⋅y$ so I can separate non-linear and linear parts:

multiplicative constraint: t = x*y,
linear constraint: z = t + x.

4.1 Witness and Parameters

/// Witness for z = x*y + x in F_p.
#[derive(Clone, Debug)]
pub struct Witness {
    pub x: F,
    pub y: F,
    pub z: F,
}
 
impl Witness {
    pub fn new(x: u32, y: u32) -> Self {
        let x_f = F::from(x);
        let y_f = F::from(y);
        let z_f = x_f * y_f + x_f;
        Self { x: x_f, y: y_f, z: z_f }
    }
}
 
#[derive(Clone, Debug)]
pub struct LigeroParams {
    pub m: usize,   // number of multiplication gates
    pub n: usize,   // codeword length
    pub deg_bound: usize, // degree bound for each row polynomial
}
 
#[derive(Clone, Debug)]
pub struct Row {
    pub values: Vec<F>, // one RS codeword
}
 
#[derive(Clone, Debug)]
pub struct Tableau {
    pub params: LigeroParams,
    pub domain: Domain,
    pub rows: Vec<Row>, // rows = 4m: x, y, t, z per gate
}

4.2 Honest Tableau for `m = 1`

For one gate, I use four rows:

u_0 = encoding of x,
u_1 = encoding of y,
u_2 = encoding of t = x*y,
u_3 = encoding of z.

Each row is the evaluation of a constant polynomial (degree 0): f_x(t) = x, etc.

impl Tableau {
    /// Build an honest tableau for a single gate z = x*y + x.
    pub fn from_witness_single_gate(w: &Witness, params: LigeroParams) -> Self {
        assert_eq!(params.m, 1, "from_witness_single_gate assumes m = 1");
        let domain = Domain::new_n(params.n);
 
        let x = w.x;
        let y = w.y;
        let t = x * y;
        let z = w.z;
 
        let fx = [x];
        let fy = [y];
        let ft = [t];
        let fz = [z];
 
        let row_x = Row { values: eval_poly(&fx, &domain) };
        let row_y = Row { values: eval_poly(&fy, &domain) };
        let row_t = Row { values: eval_poly(&ft, &domain) };
        let row_z = Row { values: eval_poly(&fz, &domain) };
 
        Tableau {
            params,
            domain,
            rows: vec![row_x, row_y, row_t, row_z],
        }
    }
}

A tiny smoke test:

fn main() {
    let w = Witness::new(2, 3); // z = 2*3 + 2 = 8
    let params = LigeroParams { m: 1, n: 5, deg_bound: 1 };
 
    let tab = Tableau::from_witness_single_gate(&w, params);
    println!("Tableau rows: {:?}", tab.rows);
 
    let r = F::from(42);
 
    println!("Proximity test (V_p low-deg?): {}", tab.proximity_test(r));
    println!("Multiplication test (V_m = 0?): {}", tab.multiplication_test(r));
    println!("Linear test (constraint holds?): {}", tab.linear_test(r));
}

Output:

Tableau rows: [
  Row { values: [2, 2, 2, 2, 2] },
  Row { values: [3, 3, 3, 3, 3] },
  Row { values: [6, 6, 6, 6, 6] },
  Row { values: [8, 8, 8, 8, 8] },
]
Proximity test (V_p low-deg?): true
Multiplication test (V_m = 0?): true
Linear test (constraint holds?): true

Every row is a constant RS codeword, and all constraints hold. Good.

5. The Three Tests on the Rows of U

Now the fun part. I implement three tests on the rows, mirroring the whiteboard formulas, but adapted to my 4-rows-per-gate layout.

Proximity Test $V_p$

Definition:

Form a random linear combination of rows:

V_p = \sum_i r^i u_i

Check: is V_p a low-degree RS codeword?

Code:

impl Tableau {
    /// V_p = (1, r, r², ..., r^{rows-1}) · U
    /// Check: is V_p a low-degree (< deg_bound) RS codeword?
    pub fn proximity_test(&self, r: F) -> bool {
        let n = self.domain.len();
        let mut v_p = vec![F::from(0); n];
 
        // For each column j, take a random linear combination of row values.
        for j in 0..n {
            let mut sum = F::from(0);
            let mut power = F::from(1); // r^0, r^1, ...
 
            for row in &self.rows {
                sum = sum + row.values[j] * power;
                power = power * r;
            }
            v_p[j] = sum;
        }
 
        is_low_degree(&v_p, &self.domain, self.params.deg_bound)
    }
}

Intuition:

This test only sees code structure. It does not know whether z = x*y + x holds.
In my toy, both honest and cheating provers keep rows as constant polynomials, so they always pass proximity — by design.

Multiplication Test $V_m$

For m gates, with row layout [x_i, y_i, t_i, z_i] per gate i, I define:

V_m = Σ r^i (u_{3i-2} ⊙ u_{3i-1} − u_{3i})

and require $V_m$ to be identically zero.

impl Tableau {
    /// Multiplication test: checks all gates satisfy t_i = x_i * y_i.
    pub fn multiplication_test(&self, r: F) -> bool {
        let m = self.params.m;
        let n = self.domain.len();
        let mut v_m = vec![F::from(0); n];
 
        for j in 0..n {
            let mut sum = F::from(0);
            let mut power = F::from(1); // r^0, r^1, ...
 
            for gate in 0..m {
                let idx_x = 4 * gate;
                let idx_y = 4 * gate + 1;
                let idx_t = 4 * gate + 2;
 
                let xj = self.rows[idx_x].values[j];
                let yj = self.rows[idx_y].values[j];
                let tj = self.rows[idx_t].values[j];
 
                let diff = xj * yj - tj;
                sum = sum + power * diff;
                power = power * r;
            }
 
            v_m[j] = sum;
        }
 
        v_m.iter().all(|&v| v == F::from(0))
    }
}

If every gate satisfies t_i = x_i*y_i, then every diff is zero and V_m is identically zero.
If some gate cheats on the product, V_m becomes a non-zero polynomial in r, and only a small fraction of r make it vanish.

5.3 Linear Test $V_l$

I separate the linear part of the constraint:

z_i = t_i + x_i \quad \text{for each gate } i.

So I define:

V_l[j] = \sum_{i=0}^{m-1} r^i (z_i[j] - t_i[j] - x_i[j])

and again require it to be identically zero:

impl Tableau {
    /// Linear test: checks all gates satisfy z_i = t_i + x_i.
    pub fn linear_test(&self, r: F) -> bool {
        let m = self.params.m;
        let n = self.domain.len();
        let mut v_l = vec![F::from(0); n];
 
        for j in 0..n {
            let mut sum = F::from(0);
            let mut power = F::from(1);
 
            for gate in 0..m {
                let idx_x = 4 * gate;
                let idx_t = 4 * gate + 2;
                let idx_z = 4 * gate + 3;
 
                let xj = self.rows[idx_x].values[j];
                let tj = self.rows[idx_t].values[j];
                let zj = self.rows[idx_z].values[j];
 
                let diff = zj - tj - xj; // z - t - x = 0
                sum = sum + power * diff;
                power = power * r;
            }
 
            v_l[j] = sum;
        }
 
        v_l.iter().all(|&v| v == F::from(0))
    }
}

Now:

Multiplication test checks the non-linear part: t = x*y.
Linear test checks the linear part: z = t + x.
Proximity ensures the rows still look like proper codewords.

For m=1, you can already see how they separate concerns: change z and keep t honest, and you'll pass multiplication but fail linear.

6. Extending to Many Gates

To get closer to the talk, I need multiple coordinates (m > 1). I introduce a vector witness:

/// Vector witness for m gates: z_i should satisfy z_i = x_i * y_i + x_i.
#[derive(Clone, Debug)]
pub struct WitnessVec {
    pub xs: Vec<F>,
    pub ys: Vec<F>,
    pub zs: Vec<F>,
}
 
impl WitnessVec {
    pub fn from_xy(xs: Vec<F>, ys: Vec<F>) -> Self {
        assert_eq!(xs.len(), ys.len());
        let zs = xs.iter().zip(&ys)
            .map(|(&x, &y)| x * y + x)
            .collect();
        Self { xs, ys, zs }
    }
 
    pub fn len(&self) -> usize {
        self.xs.len()
    }
}

And a multi-gate tableau builder:

impl Tableau {
    /// Build an honest tableau for m gates using a vector witness.
    pub fn from_witness_vec(w: &WitnessVec, params: LigeroParams) -> Self {
        assert_eq!(params.m, w.len(), "params.m must match witness length");
        let domain = Domain::new_n(params.n);
        let mut rows = Vec::with_capacity(4 * params.m);
 
        for i in 0..params.m {
            let x = w.xs[i];
            let y = w.ys[i];
            let t = x * y;
            let z = w.zs[i];
 
            let fx = [x];
            let fy = [y];
            let ft = [t];
            let fz = [z];
 
            rows.push(Row { values: eval_poly(&fx, &domain) });
            rows.push(Row { values: eval_poly(&fy, &domain) });
            rows.push(Row { values: eval_poly(&ft, &domain) });
            rows.push(Row { values: eval_poly(&fz, &domain) });
        }
 
        Tableau { params, domain, rows }
    }
}

The three tests (proximity_test, multiplication_test, linear_test) already iterate over gate in 0..m, so they work unchanged.

7. A Cheating Strategy and Soundness in Numbers

With m > 1, I can finally craft a cheating prover that:

keeps all rows as valid RS codewords (so proximity passes),
keeps all linear constraints z = t + x true (so linear passes), but
breaks multiplication t = x*y on two gates in a correlated way.

7.1 Correlated Cheat across Two Gates

Let's take m = 4 gates, build an honest tableau, and then modify gates 0 and 1:

let m: usize = 4;
let params = LigeroParams { m, n: 7, deg_bound: 1 };
 
let xs: Vec<F> = (0..m).map(|_| F::from(rng.gen_range(1..F::P))).collect();
let ys: Vec<F> = (0..m).map(|_| F::from(rng.gen_range(1..F::P))).collect();
 
let w_vec = WitnessVec::from_xy(xs, ys);
let honest_tab = Tableau::from_witness_vec(&w_vec, params.clone());
 
// Make a cheating tableau
let mut cheat_tab = honest_tab.clone();
let n = cheat_tab.domain.len();
 
let delta = F::from(1); // non-zero
let idx_t0 = 4 * 0 + 2;
let idx_z0 = 4 * 0 + 3;
let idx_t1 = 4 * 1 + 2;
let idx_z1 = 4 * 1 + 3;
 
for j in 0..n {
    // Gate 0: add delta to t and z -> z0' = t0' + x0 still holds
    cheat_tab.rows[idx_t0].values[j] = cheat_tab.rows[idx_t0].values[j] + delta;
    cheat_tab.rows[idx_z0].values[j] = cheat_tab.rows[idx_z0].values[j] + delta;
 
    // Gate 1: subtract delta from t and z -> z1' = t1' + x1 still holds
    cheat_tab.rows[idx_t1].values[j] = cheat_tab.rows[idx_t1].values[j] - delta;
    cheat_tab.rows[idx_z1].values[j] = cheat_tab.rows[idx_z1].values[j] - delta;
}

Effect:

Rows are still constant polynomials (so proximity passes).
For each gate i = 0,1, we changed t_i and z_i in sync:
- t_i' = t_i ± δ,
- z_i' = z_i ± δ,
- so z_i' = t_i' + x_i still holds (linear test passes).
But the products are wrong:
- gate 0: x0*y0 - t0' = -δ,
- gate 1: x1*y1 - t1' = +δ.

What does the multiplication test see?

For each column j:

V_m[j] = \sum_{i=0}^{m-1} r^i \, \text{diff}_i[j].

So:

V_m is the same non-zero polynomial in r for every column.
It is zero iff r = 1.
If r is uniform in F_p, the cheating prover passes with probability exactly 1/p.

This is a perfect little lab example of "soundness by random linear combination".

7.2 Monte-Carlo Experiment

I wrap everything in a main and run a Monte-Carlo:

fn multigate_soundness_experiment() {
    let mut rng = rand::thread_rng();
 
    let m: usize = 4;
    let params = LigeroParams { m, n: 7, deg_bound: 1 };
 
    // Honest witness + tableau
    let xs: Vec<F> = (0..m).map(|_| F::from(rng.gen_range(1..F::P))).collect();
    let ys: Vec<F> = (0..m).map(|_| F::from(rng.gen_range(1..F::P))).collect();
    let w_vec = WitnessVec::from_xy(xs, ys);
    let honest_tab = Tableau::from_witness_vec(&w_vec, params.clone());
 
    // Cheating tableau as above...
    let mut cheat_tab = honest_tab.clone();
    // apply correlated delta tweak...
 
    // Single r sanity check
    let r_test = F::from(42);
    println!(
        "Honest (single r): prox={}, mult={}, lin={}",
        honest_tab.proximity_test(r_test),
        honest_tab.multiplication_test(r_test),
        honest_tab.linear_test(r_test),
    );
    println!(
        "Cheat  (single r): prox={}, mult={}, lin={}",
        cheat_tab.proximity_test(r_test),
        cheat_tab.multiplication_test(r_test),
        cheat_tab.linear_test(r_test),
    );
 
    // Monte-Carlo over rounds
    let trials = 5_000;
    let rounds_list = [1usize, 2, 3];
 
    println!("\nEstimating acceptance probabilities over {trials} trials:");
    for rounds in rounds_list {
        let mut honest_accept = 0usize;
        let mut cheat_accept = 0usize;
 
        for _ in 0..trials {
            let mut honest_ok = true;
            let mut cheat_ok = true;
 
            for _ in 0..rounds {
                let r = F::from(rng.gen_range(0..F::P));
 
                let honest_round = honest_tab.proximity_test(r)
                    && honest_tab.multiplication_test(r)
                    && honest_tab.linear_test(r);
 
                let cheat_round = cheat_tab.proximity_test(r)
                    && cheat_tab.multiplication_test(r)
                    && cheat_tab.linear_test(r);
 
                honest_ok &= honest_round;
                cheat_ok &= cheat_round;
            }
 
            if honest_ok { honest_accept += 1; }
            if cheat_ok { cheat_accept += 1; }
        }
 
        let honest_rate = honest_accept as f64 / trials as f64;
        let cheat_rate = cheat_accept as f64 / trials as f64;
 
        println!(
            "  rounds = {rounds}: honest_accept ≈ {:.4}, cheat_accept ≈ {:.6}",
            honest_rate, cheat_rate
        );
    }
}

Running:

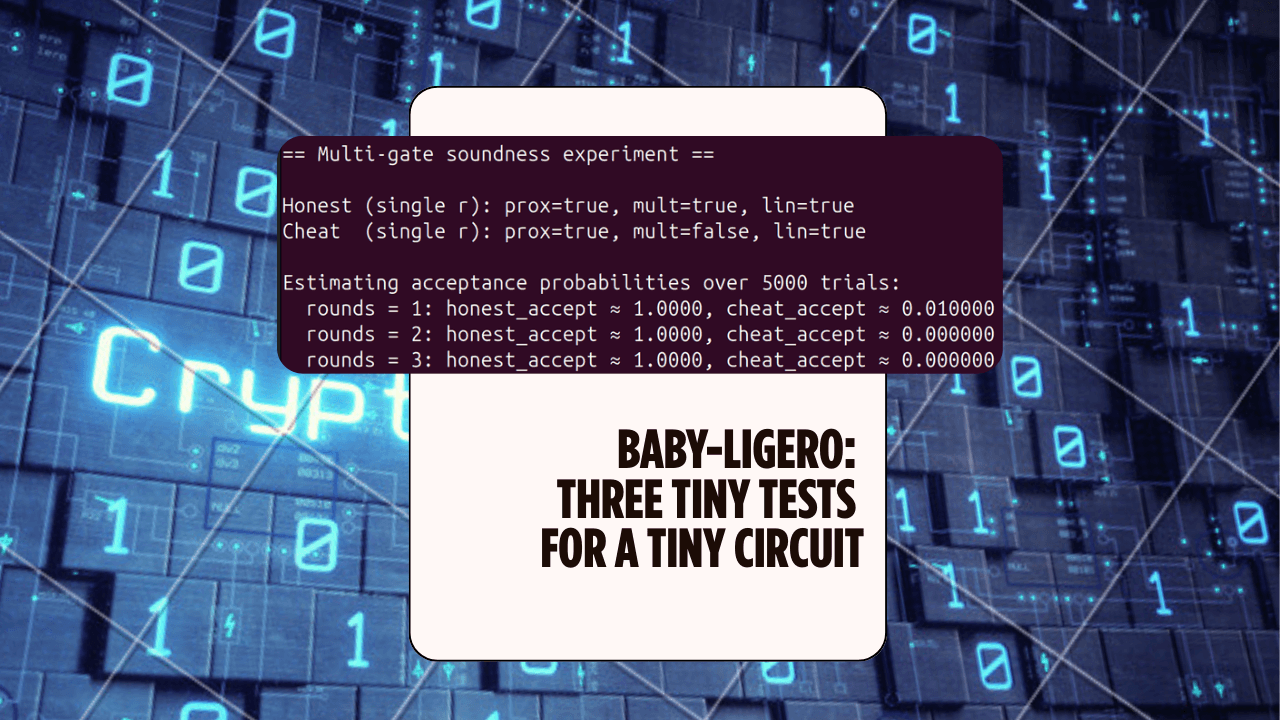
Honest (single r): prox=true, mult=true, lin=true
Cheat  (single r): prox=true, mult=false, lin=true
 
Estimating acceptance probabilities over 5000 trials:
  rounds = 1: honest_accept ≈ 1.0000, cheat_accept ≈ 0.008600
  rounds = 2: honest_accept ≈ 1.0000, cheat_accept ≈ 0.000000
  rounds = 3: honest_accept ≈ 1.0000, cheat_accept ≈ 0.000000

Interpretation:

Honest prover passes essentially always (up to floating noise).
Cheater passes about 0.0086 ≈ 1/116 in one round; with p=97 and tiny sample size, that's aligned with the theory “≈ 1/p”.
With two independent rounds, cheat acceptance drops to “essentially zero” in 5000 trials — consistent with “probability ≈ 1/p²”.

This is exactly the “soundness amplification” story Muthu tells on the board, but now I've seen it numerically.

8. How This Relates to Real Ligero

My baby lab does capture the idea of a big matrix U whose rows are codewords, as well as the three tests as random linear combinations of those rows:

V_p checks code structure (proximity).
V_m checks multiplicative constraints.
V_ℓ checks linear constraints.

It then also captures the soundness pattern: if a prover cheats but stays in the code and preserves linear constraints, the violation shows up as a non-zero polynomial in r; hitting zero by chance has probability ≈ 1/|F| per round.

It does not yet capture:

The full MPC-in-the-head construction and how you get U from secure computation views.
Packed secret sharing over larger blocks and how that interacts with RS codes.
The full constraint system A w = b and the exact hat_r construction.
Pre-processing SNARK aspects (structured reference strings, etc.).
Real-world parameter choices, noise, and “proximity” vs exact code membership.

But as a mental model, I find this baby lab very effective:

Ligero = "rows in a code + three simple random tests over those rows".

Once we've implemented those three pieces for a toy circuit, the whiteboard becomes much easier to parse.

9. References and Further Reading

Talk — ZK Hack S3M5: The Ligero Proof System, w/ Muthu Venkitasubramaniam
Paper — Ligero: Lightweight Sublinear Arguments Without a Trusted Setup (Ames–Hazay–Ishai–Venkitasubramaniam, 2022), ePrint 2022/1608.
Background on MPC & ZK:
- Zero-Knowledge from Secure Multiparty Computation — Ishai, Kushilevitz, Ostrovsky, Sahai (2007).
- Yuval Ishai, Introduction to Secure Multi-Party Computation (BIU Winter School 2020).
Polynomial commitments inspired by Ligero:
- Ligerito: A Small and Concretely Fast Polynomial Commitment Scheme — Novakovic, Angeris, 2025, ePrint 2025/1187.

Baby-Ligero: Three Tiny Tests for a Tiny Circuit — ZK Hack S3M5